a 3D cell that represents a tetrahedron More...

#include <vtkTetra.h>

Inheritance diagram for vtkTetra:

Collaboration diagram for vtkTetra:

Public Types
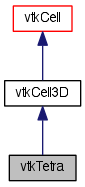
typedef vtkCell3D	Superclass
Public Member Functions
virtual const char *	GetClassName ()
virtual int	IsA (const char *type)
void	PrintSelf (ostream &os, vtkIndent indent)
int	CellBoundary (int subId, double pcoords[3], vtkIdList *pts)
int	GetParametricCenter (double pcoords[3])
double	GetParametricDistance (double pcoords[3])
int	JacobianInverse (double **inverse, double derivs[12])

virtual void	GetEdgePoints (int edgeId, int *&pts)
virtual void	GetFacePoints (int faceId, int *&pts)

int	GetCellType ()
int	GetNumberOfEdges ()
int	GetNumberOfFaces ()
vtkCell *	GetEdge (int edgeId)
vtkCell *	GetFace (int faceId)
void	Contour (double value, vtkDataArray cellScalars, vtkIncrementalPointLocator locator, vtkCellArray verts, vtkCellArray lines, vtkCellArray polys, vtkPointData inPd, vtkPointData outPd, vtkCellData inCd, vtkIdType cellId, vtkCellData *outCd)
void	Clip (double value, vtkDataArray cellScalars, vtkIncrementalPointLocator locator, vtkCellArray connectivity, vtkPointData inPd, vtkPointData outPd, vtkCellData inCd, vtkIdType cellId, vtkCellData *outCd, int insideOut)
int	EvaluatePosition (double x[3], double closestPoint, int &subId, double pcoords[3], double &dist2, double weights)
void	EvaluateLocation (int &subId, double pcoords[3], double x[3], double *weights)
int	IntersectWithLine (double p1[3], double p2[3], double tol, double &t, double x[3], double pcoords[3], int &subId)
int	Triangulate (int index, vtkIdList ptIds, vtkPoints pts)
void	Derivatives (int subId, double pcoords[3], double values, int dim, double derivs)
virtual double *	GetParametricCoords ()

virtual void	InterpolateFunctions (double pcoords[3], double weights[4])
virtual void	InterpolateDerivs (double pcoords[3], double derivs[12])
Static Public Member Functions
static vtkTetra *	New ()
static int	IsTypeOf (const char *type)
static vtkTetra *	SafeDownCast (vtkObject *o)
static void	InterpolationFunctions (double pcoords[3], double weights[4])
static void	InterpolationDerivs (double pcoords[3], double derivs[12])

static void	TetraCenter (double p1[3], double p2[3], double p3[3], double p4[3], double center[3])

static double	Circumsphere (double p1[3], double p2[3], double p3[3], double p4[3], double center[3])

static double	Insphere (double p1[3], double p2[3], double p3[3], double p4[3], double center[3])

static int	BarycentricCoords (double x[3], double x1[3], double x2[3], double x3[3], double x4[3], double bcoords[4])

static double	ComputeVolume (double p1[3], double p2[3], double p3[3], double p4[3])

static int *	GetEdgeArray (int edgeId)
static int *	GetFaceArray (int faceId)
Protected Member Functions
	vtkTetra ()
	~vtkTetra ()
Protected Attributes
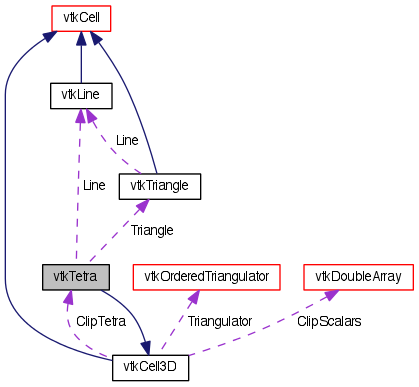
vtkLine *	Line
vtkTriangle *	Triangle

Detailed Description

a 3D cell that represents a tetrahedron

vtkTetra is a concrete implementation of vtkCell to represent a 3D tetrahedron. vtkTetra uses the standard isoparametric shape functions for a linear tetrahedron. The tetrahedron is defined by the four points (0-3); where (0,1,2) is the base of the tetrahedron which, using the right hand rule, forms a triangle whose normal points in the direction of the fourth point.

See also:: vtkConvexPointSet vtkHexahedron vtkPyramid vtkVoxel vtkWedge

Examples:: vtkTetra (Examples)

Tests:: vtkTetra (Tests)

Definition at line 45 of file vtkTetra.h.

Member Typedef Documentation

typedef vtkCell3D vtkTetra::Superclass

Reimplemented from vtkCell3D.

Definition at line 49 of file vtkTetra.h.

Constructor & Destructor Documentation

vtkTetra::vtkTetra ( ) [protected]

vtkTetra::~vtkTetra ( ) [protected]

Member Function Documentation

static vtkTetra* vtkTetra::New ( ) [static]

Create an object with Debug turned off, modified time initialized to zero, and reference counting on.

Reimplemented from vtkObject.

virtual const char* vtkTetra::GetClassName ( ) [virtual]

Reimplemented from vtkCell3D.

static int vtkTetra::IsTypeOf ( const char * name ) [static]

Return 1 if this class type is the same type of (or a subclass of) the named class. Returns 0 otherwise. This method works in combination with vtkTypeMacro found in vtkSetGet.h.

Reimplemented from vtkCell3D.

virtual int vtkTetra::IsA ( const char * name ) [virtual]

Return 1 if this class is the same type of (or a subclass of) the named class. Returns 0 otherwise. This method works in combination with vtkTypeMacro found in vtkSetGet.h.

Reimplemented from vtkCell3D.

static vtkTetra* vtkTetra::SafeDownCast ( vtkObject * o ) [static]

Reimplemented from vtkCell3D.

void vtkTetra::PrintSelf	(	ostream &	os,
		vtkIndent	indent
	)		`[virtual]`

Methods invoked by print to print information about the object including superclasses. Typically not called by the user (use Print() instead) but used in the hierarchical print process to combine the output of several classes.

Reimplemented from vtkCell3D.

virtual void vtkTetra::GetEdgePoints	(	int	edgeId,
		int *&	pts
	)		`[virtual]`

See vtkCell3D API for description of these methods.

Implements vtkCell3D.

virtual void vtkTetra::GetFacePoints	(	int	faceId,
		int *&	pts
	)		`[virtual]`

See vtkCell3D API for description of these methods.

Implements vtkCell3D.

int vtkTetra::GetCellType ( ) [inline, virtual]