---

vtkOrderedTriangulator Class Reference

helper class to generate triangulations. More...

#include <vtkOrderedTriangulator.h>

Inheritance diagram for vtkOrderedTriangulator:

[legend]Collaboration diagram for vtkOrderedTriangulator: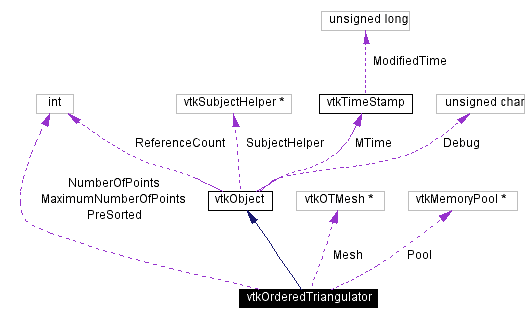

[legend]List of all members.

Public Methods
virtual const char *	GetClassName ()
virtual int	IsA (const char *type)
void	PrintSelf (ostream &os, vtkIndent indent)
void	InitTriangulation (float bounds[6], int numPts)
vtkIdType	InsertPoint (vtkIdType id, float x[3], int type)
void	Triangulate ()
void	UpdatePointType (vtkIdType internalId, int type)
vtkIdType	GetTetras (int classification, vtkUnstructuredGrid *ugrid)
vtkIdType	AddTetras (int classification, vtkUnstructuredGrid *ugrid)
vtkIdType	AddTetras (int classification, vtkCellArray *connectivity)
virtual void	SetPreSorted (int)
virtual int	GetPreSorted ()
virtual void	PreSortedOn ()
virtual void	PreSortedOff ()
Static Public Methods
int	IsTypeOf (const char *type)
vtkOrderedTriangulator *	SafeDownCast (vtkObject *o)
vtkOrderedTriangulator *	New ()
Protected Methods
	vtkOrderedTriangulator ()
	~vtkOrderedTriangulator ()

---

Detailed Description

helper class to generate triangulations.

Date:

2001/10/11 13:36:18

Revision:

1.13

This class is used to generate unique triangulations of points. The uniqueness of the triangulation is controlled by the id of the inserted points in combination with a Delaunay criterion. The class is designed to be very fast and uses block memory allocations to support rapid triangulation generation. Also, the assumption behind the class is that a maximum of hundreds of points are to be triangulated. If you desire more robust triangulation methods use vtkPolygon::Triangulate(), vtkDelaunay2D, or vtkDelaunay3D.

Background: Delaunay triangulations are unique assuming a random distribution of input points. The 3D Delaunay criterion is as follows: the circumsphere of each tetrahedron contains no other points of the triangulation except for the four points defining the tetrahedron. In application this property is hard to satisfy because objects like cubes are defined by eight points all sharing the same circumsphere (center and radius); hence the Delaunay triangulation is not unique. These so-called degenerate situations are typically resolved by arbitrary selecting a triangulation. This code does something different: it resolves degenerate triangulations by modifying the "InCircumsphere" method to use a slightly smaller radius. Hence, degenerate points are always considered "out" of the circumsphere. This, in combination with an ordering (based on id) of the input points, guarantees a unique triangulation.

There is another related characteristic of Delaunay triangulations. Given a N-dimensional Delaunay triangulation, points lying on a (N-1) dimensional plane also form a (N-1) Delaunay triangulation. This means for example, that if a 3D cell is defined by a set of (2D) planar faces, then the face triangulations are Delaunay. Combinaing this with the method to generate unique triangulations described previously, the triangulations on the face are guaranteed unique. This fact can be used to triangulate 3D objects in such a way to guarantee compatible face triangulations. This is a very useful fact for parallel processing, or performing operations like clipping that require compatible triangulations across 3D cell faces. (See vtkClipVolume for an example.)

Warning:

Duplicate vertices will be ignored, i.e., if two points have the same coordinates the second one is discarded. The implications are that the user of this class most prevent duplicate points. Because the precision of this algorithm is double, it's also a good idea to merge points that are within some epsilon of one another.

See also:

vtkDelaunay2D vtkDelaunay3D vtkPolygon

Definition at line 103 of file vtkOrderedTriangulator.h.

---

Constructor & Destructor Documentation

vtkOrderedTriangulator::vtkOrderedTriangulator (    )  [protected]

vtkOrderedTriangulator::~vtkOrderedTriangulator (    )  [protected]

---

Member Function Documentation

virtual const char* vtkOrderedTriangulator::GetClassName (    )  [virtual]

Return the class name as a string. This method is defined in all subclasses of vtkObject with the vtkTypeMacro found in vtkSetGet.h. Reimplemented from vtkObject.

int vtkOrderedTriangulator::IsTypeOf (  const char *    type )  [static]

Return 1 if this class type is the same type of (or a subclass of) the named class. Returns 0 otherwise. This method works in combination with vtkTypeMacro found in vtkSetGet.h. Reimplemented from vtkObject.

virtual int vtkOrderedTriangulator::IsA (  const char *    type )  [virtual]

Return 1 if this class is the same type of (or a subclass of) the named class. Returns 0 otherwise. This method works in combination with vtkTypeMacro found in vtkSetGet.h. Reimplemented from vtkObject.

vtkOrderedTriangulator* vtkOrderedTriangulator::SafeDownCast (  vtkObject *    o )  [static]

Will cast the supplied object to vtkObject* is this is a safe operation (i.e., a safe downcast); otherwise NULL is returned. This method is defined in all subclasses of vtkObject with the vtkTypeMacro found in vtkSetGet.h. Reimplemented from vtkObject.

void vtkOrderedTriangulator::PrintSelf (  ostream &    os, vtkIndent    indent )  [virtual]

Methods invoked by print to print information about the object including superclasses. Typically not called by the user (use Print() instead) but used in the hierarchical print process to combine the output of several classes. Reimplemented from vtkObject.

vtkOrderedTriangulator* vtkOrderedTriangulator::New (    )  [static]

Construct object. Reimplemented from vtkObject.

void vtkOrderedTriangulator::InitTriangulation (  float    bounds[6], int    numPts )

Initialize the triangulation process. Provide a bounding box and the maximum number of points to be inserted.

vtkIdType vtkOrderedTriangulator::InsertPoint (  vtkIdType    id, float    x[3], int    type )

For each point to be inserted, provide an id, a position x, and whether the point is inside (type=0), outside (type=1), or on the boundary (type=2). You must call InitTriangulation() prior to invoking this method. Make sure that the number of points inserted does not exceed the numPts specified in InitTriangulation(). Also note that the "id" can be any integer and can be greater than numPts. It is used to create tetras (in AddTetras() with the appropriate connectivity ids. The method returns an internal id that can be used prior to the Triangulate() method to update the type of the point with UpdatePointType().

void vtkOrderedTriangulator::Triangulate (    )

Perform the triangulation. (Complete all calls to InsertPoint() prior to invoking this method.)

void vtkOrderedTriangulator::UpdatePointType (  vtkIdType    internalId, int    type )

Update the point type. This is useful when the merging of nearly coincident points is performed. The id is the internal id returned from InsertPoint(). The method should be invoked prior to the Triangulate method. The type is specified as inside (type=0), outside (type=1), or on the boundary (type=2).

virtual void vtkOrderedTriangulator::SetPreSorted (  int    )  [virtual]

Boolean indicates whether the points have been pre-sorted. If pre-sorted is enabled, the points are not sorted on point id. By default, presorted is off. (The point id is defined in InsertPoint().)

virtual int vtkOrderedTriangulator::GetPreSorted (    )  [virtual]

Boolean indicates whether the points have been pre-sorted. If pre-sorted is enabled, the points are not sorted on point id. By default, presorted is off. (The point id is defined in InsertPoint().)

virtual void vtkOrderedTriangulator::PreSortedOn (    )  [virtual]

Boolean indicates whether the points have been pre-sorted. If pre-sorted is enabled, the points are not sorted on point id. By default, presorted is off. (The point id is defined in InsertPoint().)

virtual void vtkOrderedTriangulator::PreSortedOff (    )  [virtual]

Boolean indicates whether the points have been pre-sorted. If pre-sorted is enabled, the points are not sorted on point id. By default, presorted is off. (The point id is defined in InsertPoint().)

vtkIdType vtkOrderedTriangulator::GetTetras (  int    classification, vtkUnstructuredGrid *    ugrid )

Initialize and add the tetras and points from the triangulation to the unstructured grid provided. New points are created and the mesh is allocated. (This method differs from AddTetras() in that it inserts points and cells; AddTetras only adds the tetra cells.) The tetrahdera added are of the type specified (0=inside,1=outside,2=all). Inside tetrahedron are those whose points are classified "inside" or on the "boundary." Outside tetrahedron have at least one point classified "outside." The method returns the number of tetrahedrahedron of the type requested.

vtkIdType vtkOrderedTriangulator::AddTetras (  int    classification, vtkUnstructuredGrid *    ugrid )

Add the tetras to the unstructured grid provided. The unstructured grid is assumed to have been initialized (with Allocate()) and points set (with SetPoints()). The tetrahdera added are of the type specified (0=inside,1=outside,2=all). Inside tetrahedron are those whose points are classified "inside" or on the "boundary." Outside tetrahedron have at least one point classified "outside." The method returns the number of tetrahedrahedron of the type requested.

vtkIdType vtkOrderedTriangulator::AddTetras (  int    classification, vtkCellArray *    connectivity )

Add the tetrahedra classified (0=inside,1=outside) to the connectivity list provided. Inside tetrahedron are those whose points are all classified "inside." Outside tetrahedron have at least one point classified "outside." The method returns the number of tetrahedron of the type requested.

---

The documentation for this class was generated from the following file:

• Common/vtkOrderedTriangulator.h

---