Main Page Class Hierarchy Alphabetical List Compound List File List Compound Members File Members Related Pages
vtkRecursiveDividingCubes Class Reference
create points lying on isosurface (using recursive approach).
More...
#include <vtkRecursiveDividingCubes.h>
Inheritance diagram for vtkRecursiveDividingCubes:
 [legend]Collaboration diagram for vtkRecursiveDividingCubes:
[legend]Collaboration diagram for vtkRecursiveDividingCubes: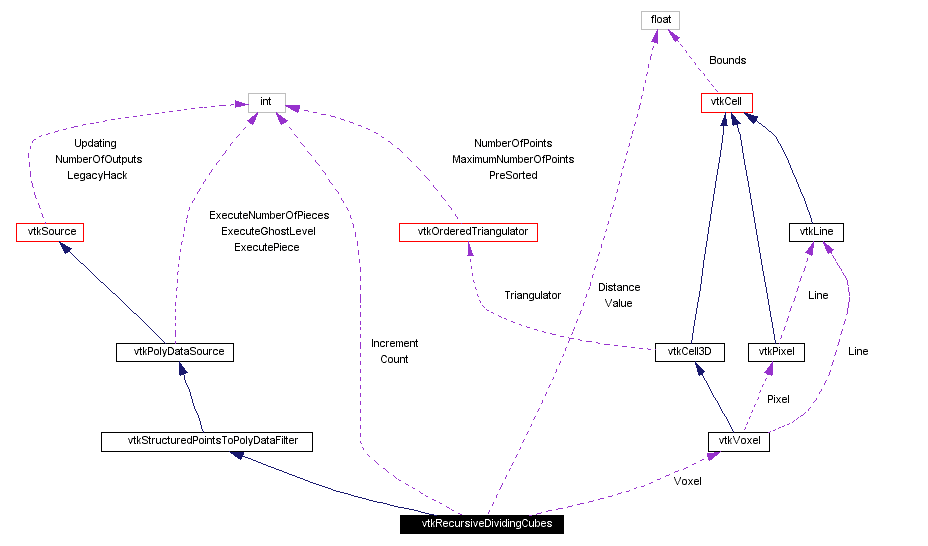 [legend]List of all members.
[legend]List of all members.
Detailed Description
create points lying on isosurface (using recursive approach).
-
Date:
-
2001/10/11 13:37:13
-
Revision:
-
1.33
vtkRecursiveDividingCubes is a filter that generates points lying on a surface of constant scalar value (i.e., an isosurface). Dense point clouds (i.e., at screen resolution) will appear as a surface. Less dense clouds can be used as a source to generate streamlines or to generate "transparent" surfaces.
This implementation differs from vtkDividingCubes in that it uses a recursive procedure. In many cases this can result in generating more points than the procedural implementation of vtkDividingCubes. This is because the recursive procedure divides voxels by multiples of powers of two. This can over-constrain subdivision. One of the advantages of the recursive technique is that the recursion is terminated earlier, which in some cases can be more efficient.
-
See also:
-
vtkDividingCubes vtkContourFilter vtkMarchingCubes
-
Tests:
-
vtkRecursiveDividingCubes (Tests)
Definition at line 72 of file vtkRecursiveDividingCubes.h.
Constructor & Destructor Documentation
| vtkRecursiveDividingCubes::vtkRecursiveDividingCubes |
( |
|
) |
[protected] |
|
| vtkRecursiveDividingCubes::~vtkRecursiveDividingCubes |
( |
|
) |
[protected] |
|
Member Function Documentation
| vtkRecursiveDividingCubes* vtkRecursiveDividingCubes::New |
( |
|
) |
[static] |
|
|
|
Instantiate object with no start, end, or progress methods.
Reimplemented from vtkPolyDataSource. |
| virtual const char* vtkRecursiveDividingCubes::GetClassName |
( |
|
) |
[virtual] |
|
| int vtkRecursiveDividingCubes::IsTypeOf |
( |
const char * |
type |
) |
[static] |
|
|
|
Return 1 if this class type is the same type of (or a subclass of) the named class. Returns 0 otherwise. This method works in combination with vtkTypeMacro found in vtkSetGet.h.
Reimplemented from vtkStructuredPointsToPolyDataFilter. |
| virtual int vtkRecursiveDividingCubes::IsA |
( |
const char * |
type |
) |
[virtual] |
|
| vtkRecursiveDividingCubes* vtkRecursiveDividingCubes::SafeDownCast |
( |
vtkObject * |
o |
) |
[static] |
|
| void vtkRecursiveDividingCubes::PrintSelf |
( |
ostream & |
os, |
|
|
vtkIndent |
indent |
|
) |
[virtual] |
|
|
|
Methods invoked by print to print information about the object including superclasses. Typically not called by the user (use Print() instead) but used in the hierarchical print process to combine the output of several classes.
Reimplemented from vtkSource. |
| virtual void vtkRecursiveDividingCubes::SetValue |
( |
float |
|
) |
[virtual] |
|
| virtual float vtkRecursiveDividingCubes::GetValue |
( |
|
) |
[virtual] |
|
| virtual void vtkRecursiveDividingCubes::SetDistance |
( |
float |
|
) |
[virtual] |
|
|
|
Specify sub-voxel size at which to generate point. |
| virtual float vtkRecursiveDividingCubes::GetDistance |
( |
|
) |
[virtual] |
|
|
|
Specify sub-voxel size at which to generate point. |
| virtual void vtkRecursiveDividingCubes::SetIncrement |
( |
int |
|
) |
[virtual] |
|
|
|
Every "Increment" point is added to the list of points. This parameter, if set to a large value, can be used to limit the number of points while retaining good accuracy. |
| virtual int vtkRecursiveDividingCubes::GetIncrement |
( |
|
) |
[virtual] |
|
|
|
Every "Increment" point is added to the list of points. This parameter, if set to a large value, can be used to limit the number of points while retaining good accuracy. |
| void vtkRecursiveDividingCubes::Execute |
( |
|
) |
[protected, virtual] |
|
|
|
This method is the old style execute method
Reimplemented from vtkSource. |
| void vtkRecursiveDividingCubes::SubDivide |
( |
float |
origin[3], |
|
|
float |
h[3], |
|
|
float |
values[8] |
|
) |
[protected] |
|
Member Data Documentation
float vtkRecursiveDividingCubes::Value [protected]
|
|
float vtkRecursiveDividingCubes::Distance [protected]
|
|
int vtkRecursiveDividingCubes::Increment [protected]
|
|
int vtkRecursiveDividingCubes::Count [protected]
|
|
vtkVoxel* vtkRecursiveDividingCubes::Voxel [protected]
|
|
The documentation for this class was generated from the following file:
Generated on Thu Mar 28 14:41:15 2002 for VTK by
 1.2.11.1 written by Dimitri van Heesch,
© 1997-2001
1.2.11.1 written by Dimitri van Heesch,
© 1997-2001



 1.2.11.1 written by Dimitri van Heesch,
© 1997-2001
1.2.11.1 written by Dimitri van Heesch,
© 1997-2001